Harrison Brammell

Introduction

In this activity, we further explored Matlab and the symbolic math toolbox. This is an addon for that allows you to solve symbolic equations as well as manipulate them in various ways that can be useful for our exploration of signals and systems. We also learned about multiple different techniques we can apply to analyze functions in Matlab, such plotting utilities like ezplot and fplot, and numerical approaches such as vpasolve.

Procedure

4.1

For the first exercise of this lab, we began by examining the function x^2 + 7x + 6 = 0. In order to find the two solutions of the equation, we used the solve function to symbolically solve the equation. When I ran the code, MATLAB gave me the solitons of 1 and 6.

4.2

For the second exercise, we explored even more functionality of the solve function by applying it to a system of equations. The equations can be seen below. We found the solutions to be 51/16, 3/2, and 39/16.

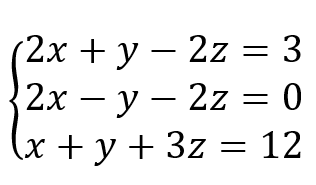
4.3

Next, we had to employ a different method to solve a problem involving circles. We were given two points on two intersecting circles and tasked with finding their center. While it may seem at first that you may need to do some math by hand in order solve this, the symbolic math toolbox does most of the work for you. We found the centers to be at (5, -4.92) and (5, 6.92).

4.4

For this section, we had to solve the equation cos(x) = x^2 – 6 using both graphical and numerical methods. Firstly, we used the ezplot function to plot both the equations and used the mouse to try and decipher the intersection points, however this was not very effective. We then used the vpasolve function to numerically find the solutions, which ended up being +/- 2.3082.

4.5

Next, we analyzed the implicit equation cos(x)=sin(x). While this equation has infinite solutions because it periodically crosses paths with itself, we applied numerical analysis functions to find the first three. Our calculations were 0.7853, 3.9269, and 7.0685.

4.6

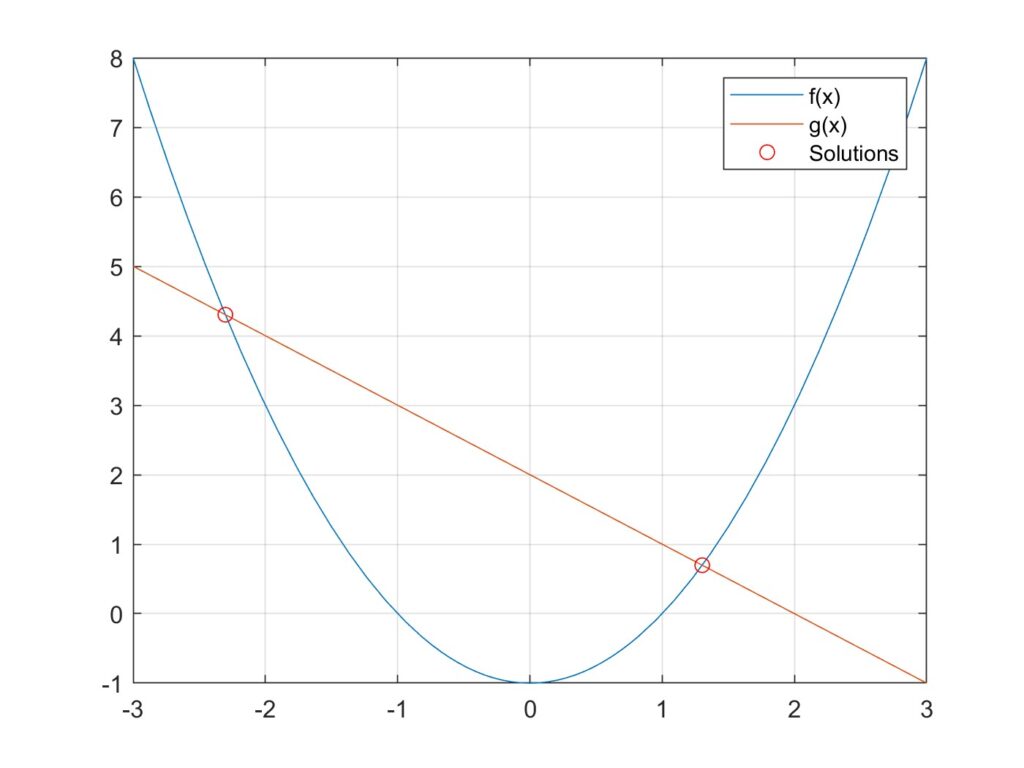
For the final section of this lab, we had to do a design project and find a relation of the form g(x)=h(x). It also had to have two real solutions and intersect at two points as well. After some trial and error, I landed on x^2 – 1 = 2 – x. Through the numerical approach, I found the solitons to be -2.30277 and 1.30277. This was confirmed graphically with the cursor, and MATLAB conveniently highlights the solution points on its own. A picture of the figure can be seen below.

Conclusion

Overall, while this lab might not have directly had a lot to do with math and concepts of signals and systems, it is still very important because it teaches us the tools we need to dive further into the subject later on. I think that the design challenge of this lab was especially challenging because it took me a while to find a function that worked, however overall, I enjoyed this activity and sharpening my skills.